Эффект доплера

Эффект Доплера в астрономии

Несомненно, без эффекта Доплера, с помощью которого произошло открытие красного смещения, мы бы не знали о крупномасштабной структуре Вселенной. Однако не только этим астрономы обязаны этому свойству волн.

Эффект Доплера позволяет обнаружить незначительные отклонения в положении звёзд, которые могут создавать планеты, обращающиеся вокруг них. Благодаря этому было открыто сотни экзопланет. Также он используется для подтверждения наличия экзопланет, предварительно обнаруженных с помощью других методов.

Двойная система коричневых карликов

Эффект Доплера сыграл решающую роль в исследовании тесных звёздных систем. Когда две звезды настолько близки, что их невозможно увидеть по-отдельности, на помощь астрономам приходит эффект Доплера. Он позволяет проследить невидимое взаимное движение звёзд по их спектру. Такие звёздные системы даже получили название «оптически двойные».

С помощью эффекта Доплера можно оценить не только скорость космического объекта, но и скорость его вращения, расширения, скорость его атмосферных потоков и многого другого. Скорость колец Сатурна, расширения туманностей, пульсации звёзд – всё это измерена благодаря этому эффекту. С помощью него даже определяют температуру звёзд, ведь температура также являет собой показатель движения. Можно сказать, что практически всё, что связано со скоростями космических объектов, современные астрономы измеряют, использую именно эффекту Доплера.

2 Релятивистский эффект Доплера

В случае электромагнитных волн формулу для частоты выводят из уравнений специальной теории относительности. Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя.

                                                              (2.5)

где с  скорость света, v  относительная скорость приёмника и источника (положительная в случае их удаления друг от друга), θ — угол между волновым вектором и скоростью источника.

Релятивистский эффект Доплера обусловлен двумя причинами:

классический аналог изменения частоты при относительном движении источника и приёмника;

релятивистское замедление времени.

Последний фактор приводит к поперечному эффекту Доплера, когда угол между волновым вектором и скоростью источника равен θ = π / 2. В этом случае изменение частоты является релятивистским эффектом, не имеющим классического аналога.

Если источник звука и наблюдатель движутся друг относительно друга, частота звука, воспринимаемого наблюдателем, не совпадает с частотой источника звука. Это явление, открытое в 1842 г., носит название эффекта Доплера.

Звуковые волны распространяются в воздухе (или другой однородной среде) с постоянной скоростью, которая зависит только от свойств среды. Однако, длина волны и частота звука могут существенно изменяться при движении источника звука и наблюдателя .

Рассмотрим простой случай, когда скорость источника υИ и скорость наблюдателя υН относительно среды направлены вдоль прямой, которая их соединяет. За положительное направление для υИ и υН можно принять направление от наблюдателя к источнику. Скорость звука υ всегда считается положительной.

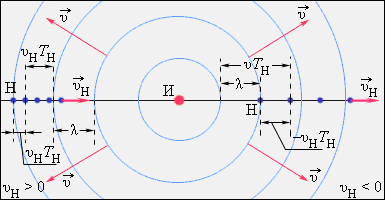
Рисунок 2.2 Эффект Доплера, случай движущегося наблюдателя, последовательные положения наблюдателя показаны через период TН звука, воспринимаемого наблюдателем

Рисунок 2.2 иллюстрирует эффект Доплера в случае движущегося наблюдателя и неподвижного источника. Период звуковых колебаний, воспринимаемых наблюдателем, обозначен через TН. Из рисунка 2.2 следует:

                                                                                (2.6)

Принимая во внимание    и  получим:

                                                                (2.7)

Если наблюдатель движется в направлении источника (υН > 0), то fН > fИ, если наблюдатель движется от источника (υН Н И.

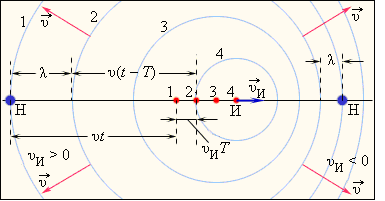
Рисунок 2.3 Эффект Доплера, случай движущегося источника, последовательные положения источника показаны через период T звука, излучаемого источником

На рисунке 2.3 наблюдатель неподвижен, а источник звука движется с некоторой скоростью υИ. В этом случае согласно рисунку 2.3 справедливо соотношение:

                   или                               (2.8)

Где     и  

Отсюда следует:

                                                                                  (2.9)

Если источник удаляется от наблюдателя, то υИ > 0 и, следовательно, fН fИ. Если источник приближается к наблюдателю, то υИ fН > fИ.

В общем случае, когда и источник, и наблюдатель движутся со скоростями υИ и υН, формула для эффекта Доплера приобретает вид:

                                                                                   (2.10)

Это соотношение выражает связь между fН и fИ. Скорости υИ и υН всегда измеряются относительно воздуха или другой среды, в которой распространяются звуковые волны. Это так называемый нерелятивистский Доплер-эффект.

В случае электромагнитных волн в пустоте (свет, радиоволны) также наблюдается эффект Доплера. Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость υ источника и наблюдателя. Выражение для релятивистского Доплер-эффекта имеет вид:

                                                                                  (2.11)

где c скорость света. Когда υ > 0, источник удаляется от наблюдателя и fН fИ, в случае υ fН > fИ.

Доплер-эффект широко используется в технике для измерения скоростей движущихся объектов («доплеровская локация» в акустике, оптике и радио) .

Искусство и культура

• В научно-фантастической литературе часто упоминается при совершении гиперпространственных полётов космических кораблей (звездолётов).
• В 6-й серии 1-го сезона американского комедийного телесериала «The Big Bang Theory» доктор Шелдон Купер идёт на Хэллоуин, для которого надел костюм, иллюстрирующий эффект Доплера. Однако все присутствующие (кроме друзей) думают, что он — зебра.
• Одно из дополнений компьютерной игры Half-Life называется Blue Shift (синее смещение), что двусмысленно (имеет и научное значение, описанное в данной статье, и также может быть переведено как «синяя смена», что является отсылкой к синей униформе охранников, одним из которых является протагонист).
• У исполнителя The Algorithm (англ.)русск. есть альбом The Doppler Effect.
• В начале клипа на песню «DNA» корейской музыкальной группы Bangtan Boys всплывает формула эффекта Доплера, в то время как сама сцена представляет собой его упрощенную иллюстрацию. Это не что иное, как шутка над фанатами, которые постоянно строят теории относительно музыкальных видео группы.

Ударные волны

Один из распространенных примеров механической волны — звуковая волна (см. гл. 6). В этом случае максимальная скорость колебаний отдельной молекулы воздуха составляет несколько сантиметров в секунду даже для достаточно большой интенсив­ности, т. е. значительно меньше скорости распространения волны (скорость звука в воздухе около 300 м/с). Это соответствует, как принято говорить, малым возмущениям среды.

Однако при больших возмущениях (взрыв, сверхзвуковое дви­жение тел, мощный электрический разряд и т. п.) скорость колеб­лющихся частиц среды может уже стать сравнимой со скоростью звука, возникает ударная волна.

При взрыве высоконагретые продукты, обладающие большой плотностью, расширяются и сжимают слои окружающего возду­ха. С течением времени объем сжатого воздуха возрастает. Тонкую переходную область, которая отделяет сжатый воздух от невозмущенного, в физике называют ударной волной. Схематич­но скачок плотности газа при распространении в нем ударной вол­ны показан на рис. 5.22, а. Для сравнения на этом же рисунке показано изменение плотности среды при прохождении звуковой волны (рис. 5.22, б).

Ударная волна может обладать значительной энергией, так, при ядерном взрыве на образование ударной волны в окружаю­щей среде затрачивается около 50% энергии взрыва. Поэтому ударная волна, достигая биологических и технических объектов, способна причинить смерть, увечья и разрушения.

Эффектом Доплера называют изменение частоты, волн, воспринимаемых наблюдателем (приемником волн), вслед­ствие относительного движения источника волн и наблюда­теля.

Представим себе, что наблюдатель приближается со скоростью u_н к неподвижному относительно среды источнику волн. При этом он встречает за один и тот же интервал времени больше волн, чем при отсутствии движения. Это означает, что воспринимаемая час­тота n¢ больше частоты волны, испускаемой источником. Но так как длина волны, частота и скорость распространения волны связаны соотношениемили с учетом

(5.57)

Другой случай: источник волн И движется со скоростью u_и к не­подвижному относительно среды наблюдателю (рис. 5.23, а). Так как источник движется вслед за испускаемой волной, то длина вол­ны будет меньше, чем при неподвижном источнике. В самом деле, длина волны равна расстоянию между двумя точками с разностью фаз 2p. За время Т, равное одному периоду, волна распространится на расстояние l. (рис. 5.23, б), источник волн переместится на рас­стояние АВ = u_иТ. Фазы точек В и С при этом различаются на 2p; следо­вательно, расстояние между ними равно длине волны l’, образуемой при движении источника излуче­ния. Используя рис. 5.23 и зная, что ,

выполним некоторые вычис­ления:

(5.58)

В этом случае наблюдатель воспринимает волну, частота коле­баний которой

(5.59)

При одновременном движении друг к другу наблюдателя и ис­точника формула для воспринимаемой частоты получается под­становкой в формулу (5.59) n¢ вместо n:

(5.60)

Как видно из (5.60), при сближении источника волн и наблю­дателя воспринимается частота больше испускаемой. Изменив знаки у u_н и u_и в (5.60), можно получить аналогичную формулу при удалении источника от наблюдателя (приемника). Таким об­разом, можно записать общую формулу

(5.61)

где «верхние» знаки в формуле относятся к сближению источника и приемника волн, а «нижние» — соответственно к удалению.

Эффект Доплера можно использовать для определения скорос­ти движения тела в среде. Для медицинских применений это име­ет особое значение. Рассмотрим подробнее такой случай.

Пусть генератор ультразвука совмещен с приемником в виде некоторой технической системы (рис. 5.24). Техническая система неподвижна относительно среды. В среде со скоростью u движет­ся объект (тело). Генератор излучает ультразвук с частотой n_г. Движущимся объектом, как наблюдателем, воспринимается час­тота n₁, которая может быть найдена по формуле (5.57):

(5.62)

где v — скорость распространения механической волны (ультра­звука).

Ультразвуковая волна с частотой n₁ отражается движущимся объектом в сторону технической системы. Приемник воспринима­ет уже другую частоту (эффект Доплера), которую можно выра­зить, используя формулу (5.59)

, или с учетом (5.62)

(5.63)

Таким образом, разница частот равна

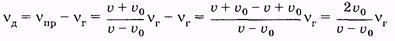(5.64)

и называется доплеровским сдвигом частоты.

В медицинских приложениях скорость ультразвука значитель­но больше скорости движения объекта (u >> u). Для этих случаев из (5.64) имеем

Эффект Доплера используется для определения скорости кро­вотока (см. § 9.5), скорости движения клапанов и стенок сердца (доплеровская эхокардиография) и других органов.

Наблюдение эффекта Доплера

Не меняющий своего местоположения микрофон записывает звук, издаваемый сиренами двух движущихся влево полицейских машин. Снизу можно видеть частоту каждого из двух звуков, принимаемую микрофоном.

Поскольку явление характерно для любых волн и потоков частиц, то его очень легко наблюдать для звука. Частота звуковых колебаний воспринимается на слух как высота звука. Надо дождаться ситуации, когда быстро движущийся автомобиль или поезд будет проезжать мимо вас, издавая звук, например, сирену или просто звуковой сигнал. Вы услышите, что когда автомобиль будет приближаться к вам, высота звука будет выше, потом, когда автомобиль поравняется с вами, резко понизится и далее, при удалении, автомобиль будет сигналить на более низкой ноте.

Что такое эффект Доплера?

Представьте себе лужу, в центре которой сидит довольный жук. Каждый раз, когда он встряхивает лапками, он создает помехи, которые перемещаются по воде. Если эти возмущения возникают в какой-то точке, то будут распространяться из этой точки во всех направлениях. Поскольку каждое возмущение движется в одной и той же среде, все они будут двигаться во всех направлениях с одинаковой скоростью.

Узор, создаваемый лапками жука, будет представлять собой серию кругов, достигающих краев лужи с одинаковой частотой. Наблюдатель в точке А (левый край лужи) увидит возмущения, бьющиеся о край лужи с той же частотой, что и наблюдатель в точке В (правый край лужи). На самом деле частота, с которой круги достигают края лужи, будет такой же, как частота, с которой жук шевелит лапками, определим ее двумя возмущениями в секунду.

Тело и кончики ног водомерок покрыты жесткими волосками, которые помогают им скользить по воде.

Теперь предположим, что жук плывет к наблюдателю В, производя возмущения с той же частотой. Поскольку насекомое движется вправо, каждое возмущение возникает ближе к наблюдателю В и дальше от наблюдателя А и, соотвественно, достигнет наблюдателя В быстрее. При этом наблюдателю В будет казаться, что частота прихода возмущений выше, чем частота, с которой эти возмущения возникают; наблюдателю А, напротив, покажется, что частота возмущений ниже, чем на самом деле. Этот пример, надеемся, неплохо иллюстрирует эффект Доплера.

Если нет, то отметим, что эффект Доплера можно наблюдать для любого типа волны – волны воды, звуковой волны, световой волны и так далее. Представьте, что вам навстречу движется полицейская машина. Когда автомобиль приближается к вам с включенной сиреной, звук сирены становится громче, но становится тише, по мере того, как машина проезжает мимо. Это – еще один пример эффекта Доплера – явного сдвига частоты звуковой волны, создаваемой движущимся источником.

Суть эффекта Доплера

Самый популярный и простой пример, объясняющий суть эффекта Доплера – неподвижный наблюдатель и машина с сиреной. Допустим, вы стоите на остановке. К вам по улице движется карета скорой помощи со включенной сиреной. Частота звука, которую вы будете слышать по мере приближения машины, не одинакова.

Сначала звук будет более высокой частоты, когда машина поравняется с остановкой. Вы услышите истинную частоту звука сирены, а по мере удаления частота звука будет понижаться. Это и есть эффект Доплера.

Эффект Доплера

Если у Кэпа спросят, кто открыл эффект Доплера, он не задумываясь ответит, что это сделал Доплер. И будет прав. Данное явление, теоретически обоснованное в 1842 году австрийским физиком Кристианом Доплером, было впоследствии названо его именем. Сам Доплер вывел свою теорию, наблюдая за кругами на воде и предположив, что наблюдения можно обобщить для всех волн. Экспериментально подтвердить эффект Доплера для звука и света удалось позднее.

Выше мы рассмотрели пример Эффект Доплера для звуковых волн. Однако эффект Доплера справедлив не только для звука. Различают:

• Акустический эффект Доплера;
• Оптический эффект Доплера;
• Эффект Доплера для электромагнитных волн;
• Релятивистский эффект Доплера.

Именно эксперименты со звуковыми волнами помогли дать первое экспериментальное подтверждение этому эффекту.

Применение эффекта Доплера

Поскольку величина эффекта Доплера зависит от скорости источника волн, эта зависимость позволяет определять скорости удаленных объектов.

Например, в астрономии по доплеровскому смещению в спектрах определяются скорости звезд и галактик.

В медицине по доплеровскому смещению ультразвуковой волны определяется скорость кровотока в артериях.

На эффекте Доплера основано действие радаров, определяющих скорость движения транспортных средств.

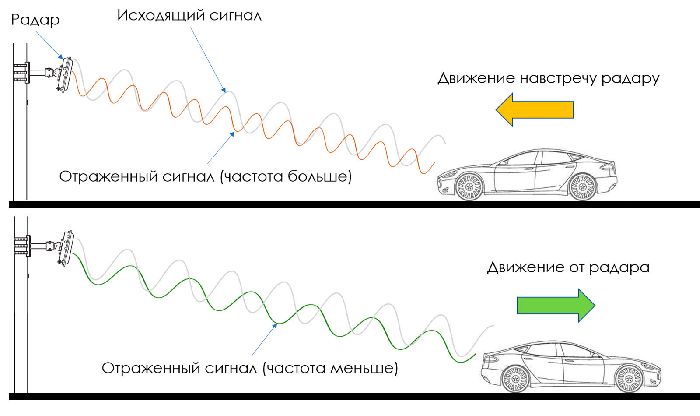
Рис. 3. Применение эффекта Доплера в радарах.

Если прислушаться к звуку проезжающего автомобиля, можно заметить, что тон его заметно меняется. При приближении он выше, при удалении – ниже. Это также проявление эффекта Доплера.

Что мы узнали?

Эффект Доплера – это изменение длины волны, испускаемой движущимся объектом. Данное явление присуще всем волновым процессам. С помощью эффекта Доплера наблюдатель может вычислить скорость перемещения источника волн, что используется во многих областях науки и техники.

Тест по теме

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Рекомендации

1. ^
2. ^
3. Алек Иден В поисках Кристиана Доплера, Springer-Verlag, Wien 1992. Содержит факсимильное издание с английский перевод.
4. Беккер (2011). Барбара Дж. Беккер, Unraveling Starlight: Уильям и Маргарет Хаггинс и подъем новой астрономии, иллюстрированное издание, Издательство Кембриджского университета, 2011; ISBN 110700229X, 9781107002296.
5. ^
6. Дауни, Нил А., «Вакуумные базуки, Electric Rainbow Jelly и 27 других проектов для Saturday Science», Принстон (2001) ISBN 0-691-00986-4
7. Это различие ясно показано в
8. Отличный обзор темы в технических деталях представлен здесь:
9. Evans, D. H .; МакДикен, В. Н. (2000). Допплерография (2-е изд.). Нью-Йорк: Джон Уайли и сыновья. ISBN 978-0-471-97001-9.[страница нужна]
10. Отилия Попескуй, Джейсон С. Харрис и Димитри Попескуз, Проектирование подсистемы связи для миссий наноспутников CubeSat: оперативные перспективы и перспективы реализации, 2016 г., IEEE
11. Арндт, Д. (2015). О моделировании каналов для наземного мобильного спутникового приема (докторская диссертация).

Ссылки [ править ]

1. ^ Джордано, Николас (2009). . Cengage Learning. С. 421–424. ISBN
2. ^ Поссель, Маркус (2017). . Эйнштейн Онлайн, Vol. 5 . Институт гравитационной физики Макса Планка, Потсдам, Германия. Архивировано из 14 сентября 2017 года . Проверено 4 сентября 2017 года .
3. Хендерсон, Том (2017). . Учебник по физике . Кабинет физики . Проверено 4 сентября 2017 года .
4. Алек Иден В поисках Кристиана Доплера , Springer-Verlag, Wien 1992. Содержит факсимильное издание с английским переводом.
5. Беккер (2011). Барбара Дж. Беккер, Распутывание звездного света: Уильям и Маргарет Хаггинс и подъем новой астрономии , иллюстрированное издание, Cambridge University Press , 2011; ISBN 110700229X , 9781107002296. 
6. ^ Розен, Джо; Готард, Лиза Куинн (2009). . Издание информационной базы. п. 155. ISBN
7. Strutt (лорд Рэлей), Джон Уильям (1896). MacMillan & Co (ред.). . 2 (2-е изд.). Макмиллан. п. 154.
8. Дауни, Neil A, «Вакуумные базуки, Электрическая Радуга желе и 27 других проекты в субботу науки», Принстон (2001) ISBN 0-691-00986-4 
9. Агарвал, Саураб; Гаурав, Ашиш Кумар; Нирала, Мехул Кумар; Синха, Саян (2018). «Потенциальная и основанная на выборке звезда RRT для динамического планирования движения в реальном времени с учетом импульса в функции затрат». Обработка нейронной информации . Конспект лекций по информатике. 11307 . С. 209–221. DOI . ISBN
10. . astro.ucla.edu .
11. Это различие ясно показано у Харрисона, Эдварда Роберта (2000). (2-е изд.). Издательство Кембриджского университета. стр. 306 и далее . ISBN
12. Превосходный обзор темы с техническими подробностями приведен здесь: Персиваль, Уилл; Самушия, Ладо; Росс, Эшли; Шапиро, Чарльз; Ракканелли, Альвизе (2011). . Философские труды Королевского общества . 369 (1957): 5058–67. Bibcode . DOI . PMID .
13. Вольф, дипл. Инж. (FH) Кристиан. . radartutorial.eu . Проверено 14 апреля 2018 года .
14. Дэвис, MJ; Newton, JD (2 июля 2017 г.). «Неинвазивная визуализация в кардиологии для широкого профиля». Британский журнал госпитальной медицины . 78 (7): 392–398. DOI . PMID .
15. Appis, AW; Трейси, MJ; Файнштейн, С.Б. (1 июня 2015 г.). . Эхо-исследования и практика . 2 (2): R55–62. DOI . PMC . PMID .
16. Эванс, DH; МакДикен, WN (2000). Допплерография (2-е изд.). Нью-Йорк: Джон Уайли и сыновья. ISBN 978-0-471-97001-9.требуется страница
17. Otilia Popescuy, Jason S. Harrisz и Димитрия C. Popescuz, Проектирование коммуникативную Тион Sub-System для наноспутников Cubesat миссий: Оперативные и реализации перспективы, 2016, IEEE
18. Qingchong, Лю (1999), «измерение доплеровского и компенсации в области мобильных систем спутниковой связи», Military связи Труды конференции / MILCOM , 1 : 316-320, CiteSeerX , DOI , ISBN
19. Оберг, Джеймс (4 октября 2004). . IEEE Spectrum .
20. ↑ Arndt, D. (2015). О моделировании каналов для наземного мобильного спутникового приема (докторская диссертация).
21. . Мир физики . 10 марта 2011 г.
22. Ши, Сихан; Линь, Сяо; Каминер, Идо; Гао, Фэй; Ян, Чжаоджу; Joannopoulos, John D .; Солячич, Марин; Чжан, Байле (октябрь 2018 г.). «Сверхлегкий обратный эффект Доплера». Физика природы . 14 (10): 1001–1005. arXiv . Bibcode . DOI . ISSN . S2CID .

Эффект Доплера для электромагнитных волн

Рассмотренное в механике (см. , §1.6 ) изменение частоты звуковых сигналов, обусловленное эффектом Доплера, определяется скоростями движения источника и приемника относительно среды, являющейся носителем звуковых волн. Для электромагнитных же волн особой среды, которая служила бы их носителем, нет. Поэтому доплеровское смещение частоты электромагнитных волн (сигналов) определяется только скоростью источника относительно приемника.

Пусть в — системе отсчета находится неподвижный приемник (рис.). К нему с релятивистской скоростью приближается — источник периодических электромагнитных (или световых) сигналов. В
— системе отсчета, связанной с источником, сигналы испускаются с частотой (собственная частота). Найдем частоту
, с которой воспринимаются эти сигналы приемником.

Рис. 5

Промежуток времени между двумя последовательными сигналами (импульсами) в
— системе, связанной с источником, равен
. Поскольку источник движется со скоростью , то соответствующий промежуток времени в — системе, согласно «эффекту замедления хода движущихся часов», будет больше, а именно

(31)

(32)

(33)

продольному эффекту Доплера

Как видно из приведенного вывода, эффект Доплера для электромагнитных волн является следствием двух явлений: замедления хода движущихся часов (корень в числителе последней формулы) и «уплотнения» (или разряжения) импульсов, связанного с изменением расстояния между источником и приемником — это учтено в первом равенстве формулы ().

Рис. 6

Рассмотрим и более общий случай: в — системе источник движется со скоростью
, составляющей угол
с линией наблюдения (рис.). В этом случае в формуле () следует заменить на
, где — проекция вектора
на ось , положительное направление которой взято от к . Тогда

(34)

В процессе движения источника проекция скорости , вообще говоря, меняется, поэтому необходимо учесть эффект запаздывания. Воспринимаемая приемником частота
в момент будет обусловлена сигналами, испущенными источником в предшествующий момент
где — расстояние от источника до в момент . Поэтому значение надо брать в момент . Итак, частоте соответствует .

В отличие от акустического эффекта Доплера, при
наблюдается поперечный эффект Доплера:

(35)

В нерелятивистском случае, когда , вместо () можно считать, что , поэтому формула () не будет содержать корня
, и тогда воспринимаемая частота

(36)

(37)

Эффект Доплера нашел многочисленные практические применения. С его помощью определяют, например, скорость излучающих атомов в пучке, угловую скорость вращения Солнца. На эффекте Доплера основаны радиолокационные методы измерения: скорости самолетов, ракет, автомашин и др. Именно этот эффект позволил открыть двойные звезды: (системы, состоящие из двух звезд, движущихся вокруг общего центра масс) — объекты, которые невозможно разрешить даже
самыми мощными телескопами. С помощью эффекта Доплера Хаббл (1929г.) обнаружил явление, названное космологическим красным смещением: линии в спектре излучения внегалактических объектов смещены в сторону больших длин волн, т.е. в красноволновую часть спектра. Оно свидетельствует о том, что внегалактические объекты удаляются от нашей Галактики со скоростями, пропорциональными расстоянию до них.

Рассмотрим в заключение два примера, на применение эффекта
Доплера. Но предварительно преобразуем формулу () от частот к
длинам волн. Частота
, отсюда малое приращение
частоты:
. Подставив обе
эти формулы в (), получим

(38)

Пример 1.

Одна из спектральных линией, испускаемых, возбужденными
ионами в состоянии покоя, имеет длину волны . Если
эту линию наблюдать под углом
к пучку данных ионов, то
обнаруживается ее доплеровское смещение
, причем

. Определим скорость ионов в пучке. Так
как
, то это значит, что ионы движутся
с нерелятивистской скоростью и справедливо соотношение ().
Условие же
означает согласно (), что

, т. е. угол:
. Искомая скорость

Пример 2.

При наблюдении спектральной линии
мкм в
направлениях на противоположные края солнечного диска на его
экваторе обнаружили различие в длинах волн на
пм.
Найдем период вращения Солнца вокруг собственной оси. Так как данные края диска движутся при вращении Солнца в
пpотивополжных направлениях с одинаковой скоростью , то
доплеровское смещение этой линии будет одинаково по модулю, но
противоположно по знаку. Поэтому суммарная разность, смещенных
длин волн равна удвоенному доплеровскому смещению:

где
— угловая скорость Солнца, — его радиус (
м). Отсюда следует, что период вращения Солнца

суток

Далее:Излучение, Свойства, Вверх:Энергия, Импульс, Назад:Импульс электромагнитной

Отдел образовательных информационных технологий ЯГПУ08.02.2014

Примеры задач с решением

Пример 1

Задание. Поезд движется со скоростью 20 $\frac{м}{с}$ мимо неподвижного наблюдателя и дает сигнал с частотой 300 Гц. Каким будет изменение частоты звукового сигнала, который воспримет наблюдатель, если скорость звука считать равной 340 $\frac{м}{с}$?

Решение. Мы имеем неподвижного наблюдателя и движущийся источник звука.

Воспользуемся формулой:

\

При этом изменение частоты будет равно:

\

Вычислим изменение частоты:

\

Ответ. $\Delta {\mathbf \nu }=35,4\ Гц$

Пример 2

Задание. Длина световой волны равна ${\lambda }_0$. Источник света движется к приемнику со скоростью $v=0,1\ c$ (где $c-\ $скорость света в вакууме). Какова длина волны излучения, которую будет регистрировать спектральный прибор приемника?

Решение. Частота электромагнитного излучения, которую будет регистрировать приемник, в системе отсчета наблюдателя равна:

\

где для нашего случая $?=\pi $ (угол между направлением наблюдения и направлением скорости движения источника волн), т.е. ${\cos ?\ }=-1.$

Частотs свяжем с длинами волн при помощи формулы:

\

Формулу (2.1) преобразуем к виду:

\

Из условия задачи:$\ \frac{v}{c}=0,1$, окончательно имеем:

\

Ответ. $\lambda ={\lambda }_0\sqrt{\frac{9}{11}}\ (м)$

История открытия

Исходя из собственных наблюдений за волнами на воде, Доплер предположил, что подобные явления происходят в воздухе с другими волнами. На основании волновой теории он в 1842 году вывел, что приближение источника света к наблюдателю увеличивает наблюдаемую частоту, отдаление уменьшает её (статья «О цветном свете двойных звезд и некоторых других звезд на небесах (англ.)русск.»). Доплер теоретически обосновал зависимость частоты звуковых и световых колебаний, воспринимаемых наблюдателем, от скорости и направления движения источника волн и наблюдателя относительно друг друга. Это явление впоследствии было названо его именем.

Доплер использовал этот принцип в астрономии и провёл параллель между акустическим и оптическим явлениями. Он полагал, что все звёзды излучают белый свет, однако цвет меняется из-за их движения к или от Земли (этот эффект для рассматриваемых Доплером двойных звёзд очень мал). Хотя изменения в цвете невозможно было наблюдать с оборудованием того времени, теория о звуке была проверена уже в 1845 году. Только открытие спектрального анализа дало возможность экспериментальной проверки эффекта в оптике.

Критика публикации Доплера

Главным основанием для критики являлось то, что статья не имела экспериментальных подтверждений и была исключительно теоретической. Хотя общее объяснение его теории и вспомогательные иллюстрации, которые он привел для звука, и были верны, объяснения и девять поддерживающих аргументов об изменении цвета звёзд верны не были. Ошибка произошла из-за заблуждения, что все звёзды излучают белый свет, и Доплер, видимо, не знал об открытиях инфракрасного (У. Гершель, 1800 год) и ультрафиолетового излучения (И. Риттер, 1801 год).

Хотя к 1850 году эффект Доплера был подтверждён экспериментально для звука, его теоретическая основа вызвала острые дебаты, которые спровоцировал Йозеф Пецваль. Основные возражения Пецваля были основаны на преувеличении роли высшей математики. Он ответил на теорию Доплера своей работой «Об основных принципах волнового движения: закон сохранения длины волны», представленной на встрече Академии Наук 15 января 1852 года. В ней он утверждал, что теория не может представлять ценности, если она опубликована всего на 8 страницах и использует только простые уравнения. В своих возражениях Пецваль смешал два абсолютно разных случая движения наблюдателя и источника и движения среды. В последнем случае, согласно теории Доплера, частота не меняется.

Эффект Доплера

Экспериментальная проверка

В 1845 году голландский метеоролог из Утрехта, Христофор Хенрик Дидерик Бёйс-Баллот, подтвердил эффект Доплера для звука на железной дороге между Утрехтом и Амстердамом. Локомотив, достигший невероятной на то время скорости 40 миль/ч (64 км/ч), тянул открытый вагон с группой трубачей. Баллот слушал изменения тона во время движения вагона при приближении и удалении. В тот же год Доплер провел эксперимент, используя две группы трубачей, одна из которых двигалась от станции, а вторая оставалась неподвижной. Он подтвердил, что, когда оркестры играют одну ноту, они находятся в диссонансе. В 1846 году он опубликовал пересмотренную версию своей теории, в которой он рассматривал как движение источника, так и движение наблюдателя. Позднее в 1848 году французский физик Арман Физо обобщил работы Доплера, распространив его теорию и на свет (рассчитал смещение линий в спектрах небесных светил). В 1860 году Эрнст Мах предсказал, что линии поглощения в спектрах звёзд, связанные с самой звездой, должны обнаруживать эффект Доплера, также в этих спектрах существуют линии поглощения земного происхождения, не обнаруживающие эффект Доплера. Первое соответствующее наблюдение удалось провести в 1868 году Уильяму Хаггинсу.

Прямое подтверждение формул Доплера для световых волн было получено Г. Фогелем в 1871 году путём сравнения положений линий Фраунгофера в спектрах, полученных от противоположных краёв солнечного экватора. Относительная скорость краёв, рассчитанная по значениям измеренных Г. Фогелем спектральных интервалов, оказалась близка к скорости, рассчитанной по смещению солнечных пятен.

Анимация, иллюстрирующая, как эффект Доплера заставляет двигатель автомобиля или сирену звучать выше по высоте, когда он приближается, чем когда он отступает. Розовые круги представляют звуковые волны.

Звук сигнала проезжающей машины

Помощь по воспроизведению

Близкие и далёкие галактики

Галактика Андромеда или M31

Между близкими галактиками постоянная Хаббла практически не применима для оценки расстояний между ними. К примеру, галактика Андромеда относительно нас имеет суммарное фиолетовое смещение, так как приближается к Млечному Пути со скоростью около 150 км/с. Если мы применим к ней закон Хаббла, то она должна удаляться от нашей галактики со скоростью 50 км/с, что совсем не соответствует реальности.

Для далёких же галактик доплеровское красное смещение практически неощутимо. Их скорость удаления от нас лежит в прямой зависимости от расстояния и с небольшой погрешностью соответствует постоянной Хаббла. Так самые далёкие квазары удаляются от нас скоростью большей, чем скорость света. Как это ни странно, это не противоречит теории относительности, ведь это скорость расширяющегося пространства, а не самих объектов

Поэтому важно уметь различать доплеровское красное смещение от космологического

Также стоит отметить, в случае электромагнитных волн имеют место быть и релятивистские эффекты. Сопутствующие искажение времени и изменение линейных размеров при движении тела относительно наблюдателя также влияют на характер волны. Как и в любом случае с релятивистскими эффектам

Метод Доплера в обнаружении экзопланет

Иначе этот метод называют спектрометрическим измерением лучевой скорости звёзд. Он получил наибольшее распространение для поиска экзопланет, и эффективность его применения исключительно высока. А также, можно «увидеть» планеты-гиганты, имеющие периоды обращения до 10 лет. Двигаясь вокруг своего светила, планета раскачивает его, что вызывает доплеровское смещение в спектре звезды. С помощью этого метода определяется амплитуда колебаний радиальной скорости между звездой и одиночной планетой.  При помощи метода Доплера к концу 2012 года удалось открыть 488 планет в 379 системах планет.

Доплеровское рассеяние

Если у нас есть многолучевое распространение, передатчик излучил, где-то в пространстве было множество объектов, от которых сигнал отразился и на приемник поступают несколько лучей. 

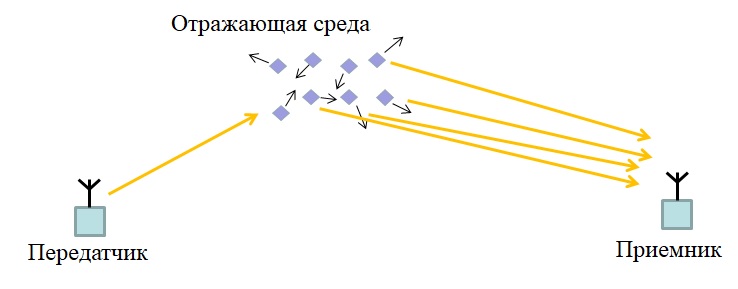
Если отражающая среда двигается, получается, что каждый луч испытывает разный сдвиг частоты. Если мы говорим про короткие волны, ионосфера это облако ионизированного газа, которое, как-то шевелится и из-за того, что к приемнику приходит несколько лучей, каждый луч испытывает разный сдвиг частоты из-за эффекта Доплера, возникает рассеяние. 

Если мы излучили сигнал с одной частотой, то на приемник придет сигнал с рассеянным спектром. 

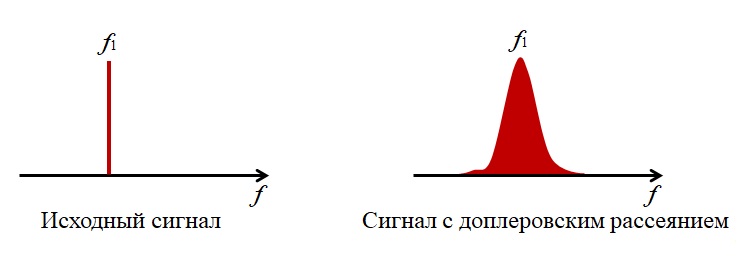
Это накладывает ограничения, приводит к искажению спектра сигнала. Если будет два сигнала близких по частоте, то в процессе рассеяния, они наползут друг на друга и будет сложно их отличить друг от друга. 

Может быть случай, когда здание неподвижно, передатчик неподвижен, движется приемник. Из-за того, что приемник движется относительно отражающих поверхностей (зданий), расстояние до каждого объекта уменьшается с разной скоростью, получаются разные углы cosθ и скорости. Соответственно, каждый луч будет испытывать сдвиг частоты, будет возникать доплеровский эффект. 

Не важно что двигается, передатчик или приемник, в любом случае возникает эффект Доплера, происходит расширение спектра и доплеровское рассеяние.