Что такое крутящий момент двигателя автомобиля

Практика

Для практических упражнений мы взяли три разных шуруповерта и два разных типа шурупов/саморезов и будем закручивать их в сухой сосновый брус, попутно фиксируя успешность операции и затраченное время.

Вот названия моделей шуруповертов и их и краткие технические характеристики:

	DeFort DCD-12-6	Bosch PSR 960	Hitachi DS 14DCL
крутящий момент, Н·м	10	12	31
частота вращения, об/мин	0-500	0-550	0-450 0-1250
аккумулятор	Ni-Cd, 12 В, 1,2 А·ч	Ni-Cd, 9,6 В, 1,2 А·ч	Li-ion, 14,4 В, 1,5А·ч

Два «старичка» (Bosch и DeFort) тут оказались неслучайно. Эти маломощные модели сразу дадут понять, насколько вся вышеизложенная теория была верна, и достаточно ли абсолютно любого шуруповерта, чтобы успешно работать с саморезами 5х90 мм и подобными. А середнячок Hitachi просто дополнит нам картину и выполнит роль некого современного инструмента.

В отношении шурупов мы мелочиться не стали и взяли для пробы тонкий черный 4,8 х 127 мм и, для полноты ощущений, мощный белый 6 х 150 мм. Чтобы закрутить последний в сосновый брус, предположительно, необходим максимальный момент около 11 Н·м.

Итак, в качестве итогов предлагаем вам посмотреть короткий видеоролик, на котором мы запечатлели весь процесс.

Тонкий саморез (4,8 х 127 мм) оказался посильной задачей для всех шуруповертов без исключения, хотя было видно, что Bosch он дался не так легко. Затраченное шуруповертами время составило: 5,3 секунды для DeFort, 7 секунд Bosch и 2,9 секунд Hitachi. Мы не ставили задачу точного сравнения времени и повторяемости, нам был важен только конечный результат. Потому мы сделали лишь по одному дублю для каждой из моделей.

Белый «крепыш» оказался по зубам уже не всем. Как и в предыдущем случае, DeFort начал очень бодро, но последний сантиметр ему так и не покорился.

Bosch, хотя и решил поставленную задачу, но запах подгоревших обмоток дал однозначно понять, что такие нагрузки этому инструменту категорически противопоказаны.

Ну а для мощного Hitachi оба самореза – как игрушки. Вот что показал секундомер: 13,3 секунд у DeFort (не довернул 1 см), 20,7 секунд Bosch и 4,3 секунды Hitachi. Вдобавок отметим, что работал Hitachi во время теста на второй скорости, где момент как минимум на треть ниже максимального заявленного в характеристиках.

Есть у нас к практической части еще одно важное замечание: в нашем тесте участвовали шуруповерты старых моделей (Hitachi не в счет), у которых нет системы защиты от перегрузки. Большинство современных моделей такую систему имеют, потому не дадут так издеваться над инструментом, как это можно наблюдать на видеоролике с шуруповертом Bosch

Это также означает, что система защиты не даст завернуть такой шуруп до конца с первого раза. Вам придется еще несколько раз включать инструмент до момента очередного срабатывания защиты (обычно это 1-2 секунды), пока шуруп не будет закручен. Но чтобы так не издеваться над инструментом, разумеется, надо покупать шуруповерт с определенным запасом мощности!

Момент электродвигателя

Мощность

связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.

Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.

Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.

Графическое представление вращающего момента электродвигателя изображено на рисунке.

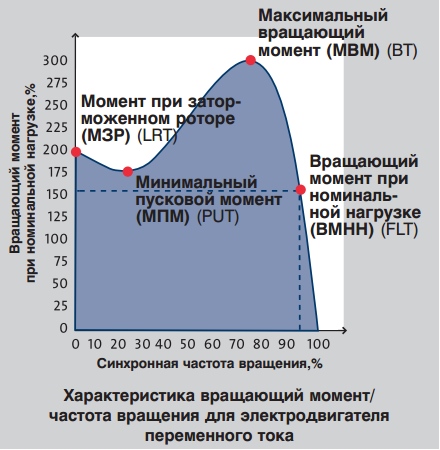
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.

Пусковой момент
(Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.

Минимальный пусковой момент
(Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.

Блокировочный момент
(Мблок): Максимальный вращающий момент — момент, который создаёт электродвигатель переменного тока с номинальным напряжением, подаваемым при номинальной частоте, без резких скачков скорости вращения. Его называют предельным перегрузочным моментом или максимальным вращающим моментом.

Вращающий момент при полной нагрузке
(Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.

Определение момента силы

Теперь перейдем к непосредственной теме статьи. Согласно физическому определению, момент силы представляет собой векторное произведение вектора приложения силы относительно оси вращения на вектор самой силы. Соответствующее математическое выражение можно записать так:

Здесь вектор r¯ направлен от оси вращения к точке приложения силы F¯.

В этой формуле вращающего момента M¯ сила F¯ может быть направлена как угодно относительно направления оси. Тем не менее параллельная оси компонента силы не будет создавать вращения, если ось жестко закреплена. В большинстве задач по физике приходится рассматривать силы F¯, которые лежат в плоскостях перпендикулярных оси вращения. В этих случаях абсолютное значение вращающего момента можно определить по следующей формуле:

Где β является углом между векторами r¯ и F¯.

Единицы измерения

Раскрывая вопрос о том, что такое момент силы, следует несколько слов сказать о его единицах измерения. Если исходить из формулы, то можно сказать, что рассматриваемая величина измеряется в ньютонах на метр и записывается сокращенно Н*м. Однако, это единица измерения совпадает с работой в физике, которая выражается в джоулях (Дж). Для описания момента сил используют именно Н*м, поскольку джоуль по своему смыслу является энергетической величиной, а не силовой характеристикой.

Если момент силы, действуя на систему, приводит к ее повороту на некоторый угол θ, то произведение этого угла в радианах на M в Н*м даст величину работы в джоулях.

Определение мощности электродвигателя по потребляемому току

Мощность двигателя можно определить по потребляемому им току. Для измерения силы тока будем использовать токоизмерительные клещи.

Перед началом измерений предварительно отключаем подачу напряжения на электродвигатель. После этого снимаем крышку с клеммной коробки и расправляем токопроводящие жилы, чтобы обеспечить удобный доступ к ним.

Затем подаем напряжение на двигатель и даем поработать в режиме номинальной нагрузки в течение нескольких минут. Устанавливаем предел измерений на значение «200 А» и токовыми клещами выполняем измерение потребляемого тока на одной из фаз. Далее замеряем напряжение на обмотках с помощью щупов, входящих в комплект токоизмерительных клещей.

Колесо выбора режимов и пределов измерений устанавливаем в позицию для измерения переменного напряжения с пределом в 750 В. Щуп красного цвета присоединяем к гнезду для измерения напряжения, сопротивления и силы тока до десяти Ампер, а черного – к гнезду «COM» . Замеры выполняем между клеммами «U1-V1» или «V1-W1» или «U1-W1» .

Расчет мощности электродвигателя выполняем по формуле:

где S – полная мощность (кВА), I – сила тока (А), U – значение линейного напряжения (кВ).

Замеряем ток на одной из фаз, а также напряжение и подставляем полученные значения в формулу (например, при замере мы получили ток равный 15,2А, а напряжение – 220В):

Важно отметить, что мощность эл. двигателя не зависит от схемы соединения обмоток статора

В этом можно убедиться, выполнив измерения на этом же двигателе, но с обмотками статора, соединенными по схеме «звезда»: измеренный ток будет равен 8,8А, напряжение – 380В. Также подставляем значения в формулу:

По этой формуле мы определили мощность электродвигателя, потребляемую из электрической сети.

Чтобы узнать мощность двигателя на валу, нужно полученное значение умножить на коэффициент мощности двигателя и на коэффициент его полезного действия. Таким образом, формула мощности двигателя выглядит так:

где P – мощность двигателя на валу; S – полная мощность двигателя; сosφ – коэффициент мощности асинхронного электродвигателя; η – КПД двигателя.

Поскольку мы не располагаем точными данными, подставим в формулу средние значения cosφ и КПД двигателя:

Таким образом, мы определили мощность электродвигателя, которая равна 4 кВт.

Мы рассказали о самых надежных методах определения мощности электродвигателя. Вы также можете посмотреть наше видео, в котором подробно показано, как определить мощность электродвигателя.

Оригинал статьи размещен на нашем сайте

Источник

Общие сведения

В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:

M→=r→×F→,{\displaystyle {\vec {M}}=\left,}

где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы.

Таблица перевода единиц измерения величин крутящего момента. Единицы момента силы, единицы вращательного момента, единицы вертящего момента, единицы вращающего момента.

Таблица перевода единиц измерения крутящего момента.

Перевести из:	Перевести в:
Н*м	Н*см	Н*мм	кН*м	Дин*м	Дин*см	Дин*мм	кгс*м	кгс*см	кгс*мм	гс*м	гс*см	гс*мм	(Унция силы)*фут	(Унция силы)*дюйм	(Фунт силы)*фут	(Фунт силы)*дюйм
Н*м (единица СИ) это:	1	102	103	10-3	105	107	108	0.1019	10.1971	101.9716	101.9716	10197.1621	101971.6212	11.8009	141.6119	7.375*10-1	8.8507
Н*см это:	10-2	1	10	10-5	103	105	106	1.0197*10-3	0.1019	1.0197	1.0197	101.9716	1019.7162	1.180*10-1	1.416	7.3756*10-3	8.8507*10-2
Н*мм это:	10-3	10-1	1	10-6	102	104	105	1.0197*10-4	1.0197*10-2	1.0197*10-1	1.0197*10-1	10.1971	101.9716	1.18*10-2	1.4161*10-1	7.3756*10-4	8.85*10-3
кН*м это:	103	105	106	1	108	1010	1011	101.9716	10197.1621	101971.6212	101971.6212	10197162.1297	101971621.2977	11800.994	141611.9289	737.5621	8850.7454
Дин*м это:	10-5	10-3	10-2	10-8	1	102	103	1.02*106	1.0197*10-4	1.0197*10-3	1.0197*10-3	1.0197*10-1	1.0197	1.1801*10-4	1.4161*10-3	7.376*10-6	8.8507*10-5
Дин*см это:	10-7	10-5	10-4	10-10	10-2	1	10	10-8	1.02*10-6	1.0197*10-5	1.0197*10-5	1.0197*10-3	1.0197*10-2	1.18*10-6	1.4161*10-5	7.4*10-8	8.85*10-7
Дин*мм это:	10-8	10-6	10-5	10-11	10-3	10-1	1	10-9	1.02*10-7	1.02*10-6	1.02*10-6	1.0197*10-4	1.0197*10-3	1.18*10-7	1.416*10-6	7*10-9	8.9*10-8
кгс*м это:	9.8066	980.665	9806.65	9.8066*10-3	980665	9806657.2*102	980665*103	1	102	103	103	105	106	115.7282	1388.7387	7.233013576	86.7961
кгс*см это:	9.8*10-2	9.8066	98.0665	9.8066*10-5	9806.65	980665	9806650	10-2	1	10	10	103	104	1.1572	13.887	7.233*10-2	8.679*10-1
кгс*мм это:	9.8*10-3	9.8*10-1	9.8066	9.807*106	980.665	98066.5	980665	10-3	10-1	1	1	102	103	1.157*10-1	1.3887	7.233*10-3	8.679*10-2
гс*м это:	9.8*10-3	9.8*10-1	9.8066	0.000009807	980.665	98066.5	980665	10-3	10-1	1	1	102	103	1.157*10-1	1.3887	7.233*10-3	8.679*10-2
гс*см это:	9.8*10-5	9.8*10-3	9.8*10-2	9.8*10-7	9.8066	980.665	9806.65	10-5	10-3	10-2	10-2	1	10	1.15*10-3	1.3887*10-2	7.233*10-5	8.679*10-4
гс*мм это:	9.8*10-6	9.8*10-4	9.8*10-3	10-8	9.8*10-1	98.0665	980.665	10-6	10-4	10-3	10-3	10-1	1	1.15*10-4	1.3887*10-3	7.233*10-6	8.679*10-5
(Унция силы)*фут это:	8.47*10-2	8.4738	84.7386	8.474*10-5	8473.8624	847386.24	8473862.4	8.641*10-3	8.64*10-1	8.6409	8.6409	864.0934	8640.9348	1	12	6.249*10-2	7.499*10-1
(Унция силы)*дюйм это:	7*10-3	7.061*10-1	7.0615	7.062*10-6	706.1552	70615.52	706155.2	7.2*10-4	7.2*10-2	7.2*10-1	7.2*10-1	72.0077	720.077906319	8.3*10-2	1	5.2083*10-3	6.2499*10-2
(Фунт силы)*фут это:	1.3558	135.5818	1355.818	1.35*10-3	135581.8	13558180	135581800	1.382*10-1	13.8254	138.2549	138.2549	13825.4959	138254.9596	16.000000189	192.000002266	1	12
(Фунт силы)*дюйм это:	1.129*10-1	11.2984	112.9848	1.129*10-4	11298.48	1129848.3	11298483.3	1.152*10-2	1.1521	11.5212	11.5212	1152.1246	11521.2466	1.333	16.000000189	8.33*10-2	1

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

|OA|=FB/FA)*|OB|=30/80*80=30 см

Ответ: расстояние ОА равно 30 см

Задача 3

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

4T = 4*100= 400 Н

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

mg=F*5/0,8=120*5/0,8=750Н

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Ловите момент! Запишите ребенка на бесплатный вводный урок в современную школу Skysmart: покажем, как у нас все устроено, определим план развития и влюбим в науку!

Примеры задач с решением

Пример 1

Задание. Каким будет единица измерения момента инерции материальной точки, которая вращается около неподвижной оси, если получить ее из основного закона динамики вращательного движения?

Решение. Формулу закона динамики вращательного движения для материальной точки представим как:

\

где $\overline{M}$ — суммарный момент сил, который действует на точку; $\overline{\varepsilon \ }$ — угловое ускорение с которым точка движется. Выразим момент инерции из (2.1):

\

тогда:

\=\frac{\left\ }{\left}\left(1.3\right),\]

Единицей измерения момента сил в системе СИ является:

\=Н\cdot м=\frac{кг\cdot м}{с^2}м=\frac{кг\cdot м^2}{с^2}.\]

Угловое ускорение материальной точки найдем как:

\

где $a_{\tau }$ — тангенциальное ускорение точки; R — радиус окружности, по которой точка перемещается.

Значит:

\=\frac{\left}{\left}=\frac{м}{с^2\cdot м}=\frac{1}{с^2}.\]

В соответствии с выражением (1.3) имеем:

\=\frac{кг\cdot м^2}{с^2}\cdot c^2=кг\cdot м^2.\]

Ответ. Исходя из основного закона динамики вращательного движения, получаем, что в системе СИ момент инерции измеряется в килограммах, умноженных на метр в квадрате.

Пример 2

Задание. Вычислите момент инерции Земного шара относительно его оси вращения. Считайте массу Земли и ее радиус известными. ($M_Z=5,97\cdot {10}^{24}кг;;\ R_Z=6371\ км$). Выразите момент инерции в $т\cdot м^2$ (тонна, умноженная на метр в квадрате)

Решение. Будем считать Землю однородным шаром. Найдем момент инерции шара, относительно оси, которая проходит через центр. Разобьем шара на диски (рис.1) толщина которых составляет $dh$, радиус ($r)\ $дисков изменяется, плоскости дисков которые перпендикулярны оси вращения.

Из рис.1 очевидно, что:

\

при этом -R$\le h\le $R.

Элементарный момент инерции (диска) запишем как:

\

где масса выделенного диска ($dm=\rho dV$) равна:

\

Следовательно:

\

Получим момент инерции шара, относительно оси, которая проходит через его центр масс, интегрируя выражение (2.4) по объему шара:

\

Плотность однородного шара равна:

\

то выражение (2.5) преобразуем к виду:

\

Окончательно формулу для нахождения момента инерции Земного шара запишем как:

\

Вычислим момент инерции Земли:

\

Для того, чтобы выразить момент инерции в $т\cdot м^2$, используем соотношение:

\

Получаем:

\

Ответ. $J=9,7\cdot {10}^{34}т\cdot м^2$

Расчет момента силы

Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

           МА=F×AB=F×3м

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:

           MB=F×cos30×AB=F×cos30×3м

Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:

           MB=F×3м

Крутящий момент и лошадиная сила

Автолюбители нередко дискутируют друг с другом: чей двигатель мощнее. Но иногда и не представляют при этом, из чего складывается данный параметр. Общепринятый термин «лошадиная сила» был введён изобретателем Джеймсом Уаттом в XVIII веке.  Он придумал его, наблюдая за лошадью, которая была запряжена в поднимающий уголь из шахты механизм. Он рассчитал, что одна лошадь за минуту может поднять 150 кг угля на высоту 30-ти метров. Одна лошадиная сила эквивалентна 735,5 Ватт, или 1 кВт равен 1,36 л.с.

В первую очередь, мощность любого мотора оценивают в лошадиных силах, и лишь потом вспоминают о крутящем моменте. Но эта тяговая характеристика тоже даёт представление о конкретных тягово-динамических возможностях автомобиля. Крутящий момент является показателем работы силового агрегата, а мощность – основным параметром выполнения этой работы. Эти показатели тесно связаны друг с другом. Чем больше производится двигателем лошадиных сил, тем больше и потенциал крутящего момента. Реализуется этот потенциал в реальных условиях через трансмиссию и полуоси машины. Соединение этих элементов вместе и определяет, как именно мощность может переходить в крутящий момент.

Простейший пример – сравнение трактора с гоночной машиной. У гоночного болида лошадиных сил много, но крутящий момент требуется для увеличения скорости через редуктор. Чтобы такая машина двигалась вперёд, надо совсем немного работы, потому что основная часть мощности используется для развития скорости.

Что касается трактора, то у него может быть мотор с таким же рабочим объёмом, который вырабатывает столько же лошадиных сил. Но мощность в этом случае используется не для развития скорости, а для выработки тяги (См. тяговый класс). Для этого она пропускается через многоступенчатую трансмиссию. Поэтому трактор не развивает высоких скоростей, зато он может буксировать большие грузы, пахать и культивировать землю, и т.д.

В двигателях внутреннего сгорания сила передаётся от газов сгорающего топлива поршню, от поршня – передаётся на кривошипный механизм, и далее на коленчатый вал. А коленвал, через трансмиссию и приводы, раскручивает колёса.

Естественно, крутящий момент двигателя не постоянен. Он сильней, когда на плечо действует бо́льшая сила, и слабей – когда сила слабнет или перестаёт действовать. То есть, когда водитель давит на педаль газа, то сила, воздействующая на плечо, повышается, и, соответственно увеличивается крутящий момент двигателя.

Мощность обеспечивает преодоление всевозможных сил, которые мешают двигаться автомобилю. Это и сила трения в двигателе, трансмиссии и в приводах автомобиля, и аэродинамические силы, и силы качения колёс и т.д. Чем больше мощность, тем большее сопротивление сил машина сможет преодолеть и развить большую скорость. Однако мощность – сила не постоянная, а зависящая от оборотов мотора. На холостом ходу мощность одна, а на максимальных оборотах – совершенно другая. Многими автопроизводителями указывается, при каких оборотах достигается максимально возможная мощность автомобиля.

Необходимо учитывать, что максимальная мощность не развивается сразу. Автомобиль стартует с места практически при минимальных оборотах (немного выше холостого хода), и для того, чтобы отмобилизировать полную мощность, требуется время. Тут и вступает в дело крутящий момент двигателя. Именно от него и будет зависеть, за какой отрезок времени автомашина достигнет своей максимальной мощности – то есть, динамика её разгона.

Зачастую водитель сталкивается с такими ситуациями, когда требуется придать автомобилю значительное ускорение для выполнения необходимого маневра. Прижимая педаль акселератора в пол, он чувствует, что автомобиль ускоряется слабо. Для быстрого ускорения нужен мощный крутящий момент. Именно он и характеризует приёмистость автомобиля.

Основную силу в двигателе внутреннего сгорания вырабатывает камера сгорания, в которой воспламеняется топливно-воздушная смесь. Она приводит в действие кривошипно-шатунный механизм, а через него – коленчатый вал. Рычагом является длина кривошипа, то есть, если длина будет больше, то и крутящий момент тоже увеличится.

Однако увеличивать кривошипный рычаг до бесконечности невозможно. Ведь тогда придётся увеличивать рабочий ход поршня, а вместе с ним и размеры двигателя. При этом уменьшатся и обороты двигателя. Двигатели с большим рычагом кривошипного механизма можно применить только лишь в крупномерных плавательных средствах. А в легковых автомашинах с небольшими размерами коленчатого вала не поэкспериментируешь.

Приведение маховых масс к одной оси

Иногда возникает необходимость приведения маховых масс электропривода к одной оси. Это приводит к удобству расчета системы электропривода, так как все моменты инерции системы приводятся как правило к валу машины.

Для начала разберемся что такое момент инерции относительно оси – это сумма произведений масс отдельных частей тела, умноженного на квадрат расстояния этой же части тела до оси вращения, которая берется для всего тела:

На практике, как правило, момент инерции довольно часто выражают как произведение квадрата радиуса инерции на массу тела:

m – общая масса всего тела, выраженная в кГсек 2 /м;

p – радиус инерции тела, выражен он в м;

Радиус инерции – расстояние от оси вращения, которая проходит через центр тяжести объекта, на котором нужно поместить массу объекта, которая будет сосредоточена в одной точке, чтоб она удовлетворяла равенству:

Значения радиусов инерции простейших геометрических тел приведены ниже. Используя формулы приведенные ниже и при условии известности массы тела, можно вычислить момент инерции тела по формулам, приведенным выше:

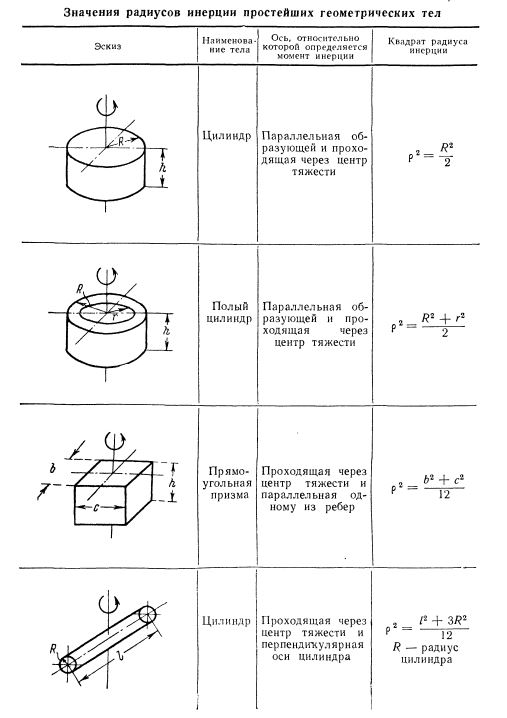
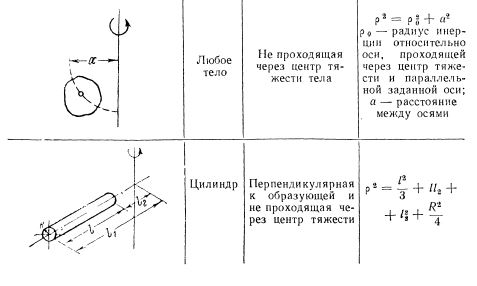
Если геометрические тела не сложные, то момент инерции можно приблизительно определить как сумму таких моментов отдельных тел , взятых относительно оси вращения. Как пример – момент инерции (далее J) маховика будет равен сумме J спиц, обода и втулки. В случаях, когда точное вычисление J представляется затруднительным, могут оперировать приближенными величинами. Иногда для маховика определяют J обода и прибавляют от 8% до 15% для учета маховых масс спиц. В случае червяка J ротора зубцов принимается 40% J пологого цилиндра соответствующих размеров. Червячное или зубчатое колесо учитывается как полый цилиндр. К полученной величине добавляют 25% для спиц и втулки. Если для зубчатого колеса известны только вес и шаг зацепления, то J могут определять как произведение 60% всего веса на квадрат радиуса длительной окружности.

Приведенный момент инерции (J_пр) входит в уравнение движения электропривода. J_пр – это J простейшей системы, которая состоит из элементов, которые вращаются со скоростью вала или оси, к которой производят приведение, и при этом запас кинетической энергии приведенной системы равен запасу кинетической энергии реальной системы.

Ниже показана реальная система и приведенная

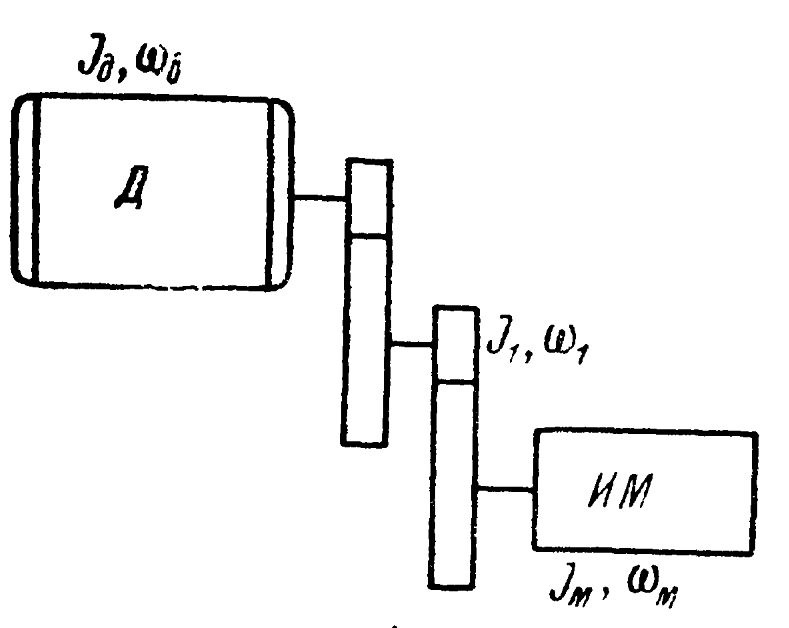
В таком случае выполнится равенство:

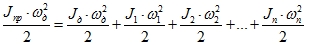
Где: J_пр – приведенный момент инерции в валу электромашины;

J₁, J₂… J_n, ω₁, ω₂, ω_n – моменты инерции и угловые скорости вращения механизмов или передач машины в соответствующих осях;

J_д, ω_д – угловая скорость и момент инерции электродвигателя.

Отсюда очевидно, что:

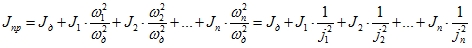
Где: j₁, j₂, …, j_n – передаточные числа между осями вращающихся звеньев и осью электромашины.

Отсюда следует, что J_пр вращающихся частей равен сумме J каждого отдельного элемента системы относительно своего вала, деленного на квадрат передаточного числа (j), между валом конкретного элемента и валом, к котором приводится момент инерции. Часто при определении J_пр системы его считают равным сумме моментов инерций ротора или якоря электрической машины и J_пр рабочего органа, а также J отдельных звеньев системы передаточного механизма учитывают с помощью увеличения J в δ раз, то есть:

Значение δ обычно лежит в пределах 1,1 ÷ 1,3.

В теории электропривода довольно часто встречается понятия махового момента – GD 2 , вместо моментов инерций. Если заменить в формуле приведенной выше массу m на вес G и ускорение свободного падения g, а радиус величины инерции p через ее диаметр D, получим следующее выражение:

GD 2 выражается в кГм 2 . Очевидно, что для GD 2 также существует соотношение, аналогичное выражению для J:

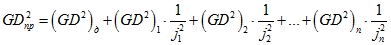
При введении вместо J в уравнение движение электропривода GD 2 получим следующее выражение:

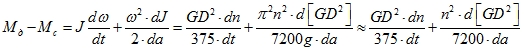
Уравнения движения с использованием GD 2 и числа оборотов в минуту могут казаться более удобными для применения на практике, так как скорость вращения вала машины обычно измеряют в оборотах в минуту — об/мин, GD 2 – довольно часто публикуют в каталогах. Однако при использовании их следует помнить, что коэффициенты 375 и 7200 – числа, имеющие размерность ускорения. Без учета этих обстоятельств правые части этих выражений не будут иметь размерность момента. Поэтому при сложных расчетах рекомендуется использовать уравнение движения в форме

Источник

Что такое мощность двигателя

Под мощностью следует понимать физическую величину, которая показывает совершаемую двигателем работу за единицу времени. При вращательном движении мощность определяется как произведение крутящего момента на угловую скорость вращения коленчатого вала. Обычно она указывается в лошадиных силах (л.с.), но встречается измерение и в кВт.

Существует несколько единиц измерения под названием «лошадиная сила», но, как правило, имеется в виду так называемая «метрическая лошадиная сила», которая равная ≈ 0,7354 кВт. А вот в США и Великобритании лошадиные силы, касающиеся автомобилей, приравнивают к 0,7456 кВт, то есть как 75 кгс*м/с, что приблизительно равно 1,0138 метрической.

• 1 кВт = 1,3596 л.с. (для метрического исчисления);
• 1 кВт = 1,3783 hp (английский стандарт);
• 1 кВт = 1,34048 л.с. (электрическая «лошадка»).

Если же конвертировать мощность 1 лошадиной силы в киловатты (в промышленности или энергетике), то она будет примерно равна 0,746 кВт. Понятие лошадиная сила не входит в международную систему измерений (СИ), поэтому измерение мощности в кВт будет более правильным.

Виды мощности

Для определения характеристик двигателя применяют такие понятия мощности как:

• индикаторная;
• эффективная;
• литровая.

Индикаторной называют мощность, с которой газы давят на поршень. То есть, не учитываются никакие другие факторы, а только давление газов в момент их сгорания. Эффективная мощность, эта та сила, которая передается коленчатому валу и трансмиссии. Индикаторная будет пропорциональной и среднему давлению газов на поршень.

Также есть параметр, называемый литровой мощность двигателя. Это соотношение объема двигателя к его максимальной мощности. Для бензиновых моторов литровая мощность составляет в среднем 30-45 кВт/л, а у дизельных – 10-15 кВт/л.

Как узнать мощность двигателя автомобиля

Конечно, значение можно посмотреть в документах на машину, но иногда требуется узнать мощность автомобиля, который подвергался тюнингу или давно находится в эксплуатации. В таких случаях не обойтись без динамометрического стенда. Его можно найти в специализированных организациях и на станциях техобслуживания. Колеса автомобиля помещаются между барабанами, создающими сопротивление вращению. Далее имитируется движение с разной нагрузкой. Компьютер сам определит мощность двигателя. Для более точного результата может понадобиться несколько попыток.