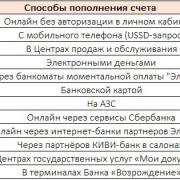
Как найти среднюю скорость

Примеры задач с решением

Пример 1

Задание. Положение материальной точки, задано радиус-вектором $\overline{r\ }\left(t\right),$ который является функцией времени: $\overline{r\ }\left(t\right)={2t}^4\overline{i}+t^2\overline{j},$ где $\overline{i}$ и $\overline{j}$ — единичные векторы осей X и Y (рис.1). Чему равен модуль скорости точки в момент времени $t=1$c?

Решение. В качестве основы для решения задачи воспользуемся формулой скорости:

\

Подставим в выражение (1.1) $\overline{r\ }\left(t\right)=t^4\overline{i}+3t^2\overline{j},$ получим:

\

Из уравнения (1.2) имеем:

\

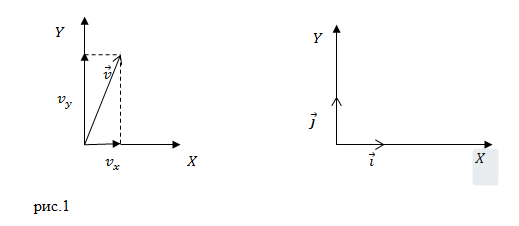
Используя теорему Пифагора, величину скорости вычислим как:

\

Ответ. $v=\sqrt{68}\frac{м}{с}$

Пример 2

Задание. С какой скоростью должен лететь самолет с востока на запад на широте $\varphi $, чтобы за окном иллюминатора всегда было светло? Радиус Земли считать равным R.

Решение. Сделаем рисунок.

Самолет летит по окружности (рис.2), радиус которой найдем как:

\

Для того чтобы не наступала ночь, тело должно двигаться с угловой скоростью, которая равна скорости вращения Земли вокруг своей оси ($\omega $). Для вычисления скорости движения самолета воспользуемся формулой:

\

Угловую скорость вращения Земли найдем, зная, что период вращения Земли составляет 24 ч ($T=24\ ч$), следовательно, величину угловой скорости вращения Земли можно считать известной и равной:

\

Окончательно получим, скорость движения самолёта равна:

\

Ответ. $v=\frac{2\pi }{T}R{\cos \varphi \ }$

Формула мгновенной скорости

Определение

Мгновенная скорость (обычно просто скорость) — это векторная величина, равная первой производной от радиус-вектора ($\overline{r}$), определяющего положение движущейся материальной точки, по времени ($t$):

\

Представим вектор $\overline{r}$ в декартовой системе координат в виде:

где $\overline{i}$; $\overline{j}$; $\overline{k}$ — единичные орты соответствующих осей координат, постоянные во времени, при этом формулой скорости можно считать выражение:

Проекциями вектора скорости на оси координат X, Y,Z являются:

Величину (модуль) скорости найдем в соответствии с формулой:

Если движение задается при помощи параметров траектории, что означает: известны траектория и функция пути от времени ($s(t)$); путь отсчитывают от точки траектории, которую считают начальной; каждая точка траектории характеризуется своей величиной $s$; радиус — вектор является функцией от $s,$ и траекторию можно задать при помощи уравнения:

в таком случае в формуле (1) $\overline{r}\left(t\right)$ будем рассматривать как сложную функцию: $\overline{r}\left$, формулой скорости станет:

Величина $\Delta s$ — это расстояние между двумя точками по траектории движения тела. Модуль $\left|\Delta \overline{r}\right|$ — расстояние между этими точками по кратчайшему направлению — прямой. При сближении рассматриваемых двух точек разница между $\Delta s$ и $\left|\Delta \overline{r}\right|$ уменьшается. Имеем:

где $\overline{\tau \ }$ — единичный вектор, касательный к траектории движения материальной точки. Кроме этого:

модуль скорости движения точки по траектории. Уравнение (6) представим как:

Формула (9) показывает, что мгновенная скорость направлена по касательной к траектории движения тела (материальной точки).

Средняя скорость автомобилей на МКАД

Определяет степень использования пробега автомобиля с грузом.

При работе автомобиля на линии различают пробеги: общий, с грузом, холостой и нулевой.

Пробег с грузом является производительным пробегом.

где: Sгp — пробег с грузом, км; Sо.пр — общий пробег автомобиля, км.

Пример. Общий пробег автомобиля за день составил 320 км, с грузом — 244 км. Определить КИПр.

Решение.

Величина коэффициента использования пробега зависит от размещения пунктов погрузки и разгрузки, характера грузопотоков и организации диспетчерской службы на линии. Водители-новаторы добиваются сокращения непроизводительных пробегов за счет перевозки попутных грузов. Например, при перевозке сахарной свеклы с поля на сахарный завод они используют обратные рейсы для перевозки на поля минеральных удобрений.

Решение.

Частные случаи нахождения средней скорости

Это задачи на нахождение средней скорости

Задачи простые, важно понять и запомнить формулу: Если участков пути было два, тогда Если три, то соответственно: *Как вы поняли, смысл таков: в знаменателе складываются отрезки времени, в числители суммируем расстояния пройденные за соответствующие им отрезки времени. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 61 км/ч, а вторую половину времени – со скоростью 87 км/ч

В правительстве обращение пока не комментируют. Ограничить скорость в населенных пунктах во вторник попросили премьера глава комитета Совета Федерации по регламенту и организации парламентской деятельности Вадим Тюльпанов и член этого комитета, экс-глава ГАИ России Владимир Федоров. Авторы обращения уверены, что снижение разрешенного лимита с 60 до 50 км/ч позволит сократить количество ДТП и уровень смертности на дорогах, а также поспособствует

. Подробнее: «По оценке экспертов, при скорости автомобиля 50 км/ч с учетом времени реакции и тормозного пути расстояние, которое проходит автомобиль до остановки, составляет 28 метров, а при скорости 60 км/ч — 36.

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

• Пусть — общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени . Аналогично, на втором участке пути тело двигалось в течение интервала времени .
• Тогда средняя скорость движения равна:

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

• Пусть — общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен: . Аналогично, путь, пройденный телом в течение второй половины времени движения, равен: .
• Тогда средняя скорость движения равна:

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Репетитор по физике на Юго-ЗападнойСергей Валерьевич

Примеры задач с решением

Пример 1

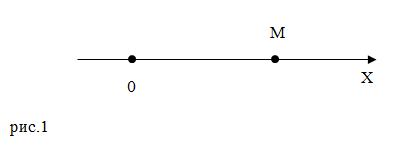
Задание: Движение точки M (рис.1) задано уравнением: $x=2t^2-4t^3$(м). Начало движения при $t=0$ c. Каким будет направление движения этой точки по отношению к оси X при 1) $t_1$=0,25 c 2) $t_2$=0,5 c.

Решение: Точка движется по оси X, следовательно, скорость найдем как:

\

Подставим выражение $x(t)$ заданное в условии задачи в формулу (1.1), получим функцию $v_x(t)$:

\

Для того чтобы определить направление скорости в конкретный момент времени подставим соответствующий момент времени в (1.2) и сравним полученный результат с нулем:

\

\[v_{x2}\left(t_2=0,5\ с\right)=4\cdot 0,5-12{\left(0,5\right)}^2=-1\ (\frac{м}{с})Ответ: 1) $v_{x1}\left(t_1=0,25\ с\right)$ направлена по оси X. 2) $v_{x2}\left(t_2=0,5\ с\right)$
направлена против оси X.
   

Пример 2

Задание: Дан закон движения материальной точки: s$=At^2+Bt$ ($A>0$ и $B>0$ — постоянные величины). Сравните среднюю скорость, полученную при использовании формулы:

\

и среднюю скорость, вычисленную как среднее арифметическое начальной и конечной скоростей в интервале времени $\left$.

Решение: Найдем величину средней скорости, используя определение:

\

и уравнение движения:

\

Для момента времени $t’\ $ имеем:

\

Получим уравнение скорости $v\left(t\right),\ $используя формулу:

\

При $t=0$ мгновенная скорость рассматриваемого нами движения равна:

\

Конечная скорость при $t=t’$:

\

Найдем среднее арифметическое начальной и конечной скоростей на заданном отрезке времени:

\

Ответ: При данном в условии задачи законе движения материальной точки средняя скорость может быть найдена как среднее арифметическое начальной скорости и конечной ($\left\langle v\right\rangle =\frac{v\left(t=0\right)+v\left(t=t’\right)}{2}$).