Расчет максимальной скорости автомобиля. расчет кпп
Содержание:
- Таблица рядов и главных пар КПП Ваз 2108-2110-1118-2170
- Расчет оборотов двигателя по передаточному числу
- Крутящий момент редуктора
- Тип редуктора
- Основные характеристики редуктора
- Звезды
- Тип редуктора
- Как рассчитать передаточное число
- muller1569 › Blog › Динамика разгона взависимости от размера и веса колеса.
- Передаточное отношение зубчатой передачи
Таблица рядов и главных пар КПП Ваз 2108-2110-1118-2170
Таблица расчета рядов и главных пар в КПП переднеприводного ВАЗ.
Позволяет подобрать ряд и главную пару под условия эксплуатации автомобиля, что существенно снизит нагрузку на двигатель и продлит его ресурс до капитального ремонта. Подобрав нужную комплектацию, используйте программу для перевода цифр в наглядные графики.
Воспользуйтесь нашим Телеграм — каналом ctoprovaz и Чатом chatprovazдля получения дополнительной информации.
Таблица главных пар КПП 2108.
Примечание: Главная пара 4.1 — разгружает двигатель, мотору легче крутить колеса, повышается динамика машины, передачи укорачиваются, максимальная скорость падает ~ на 20км/ч ( при 160 км/ч. обороты тахометра 5 тыс.), расход топлива + 1л. ( за счет изменения езды). Главная пара 4.3 -тоже, что и 4.1 + 5км/ч на всех передачах. Гл. пара 4.1 или 4.3 + спортивный ряд (06, 07 или 08-й): динамика (быстрый разгон за счет гл. пары) + длинные передачи, в основном 1-я и 2-ая раскручиваются по максимуму. Гл. пары 4.5 и 4.7: передачи еще короче, чем 4.1 и 4.3 ( максимальная скорость при 5 тыс. оборотов тахометра 140км/ч. ), рекомендуемое использование: при буксировке и перевозке тяжелых прицепов. Гл. пары 4.9, 5.1, 5.3 и 5.07: используются только на крутых склонах-подъемах ( максимальная скорость 110-120 км/ч.) Ряды: 011, 012, 018- устанавливаются со стандартной гл. парой 3.9 под форсированные двигателя 1.7, 1.8 и 2.0л. |
Понравился материал? Поделись ссылкой с друзьями…
Трансмиссия / Сделай сам / Автошкола
+16
Расчет оборотов двигателя по передаточному числу
Как рассчитать передаточное отношение шестерен механической передачи.
В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев
Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев
Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.
Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.
Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.
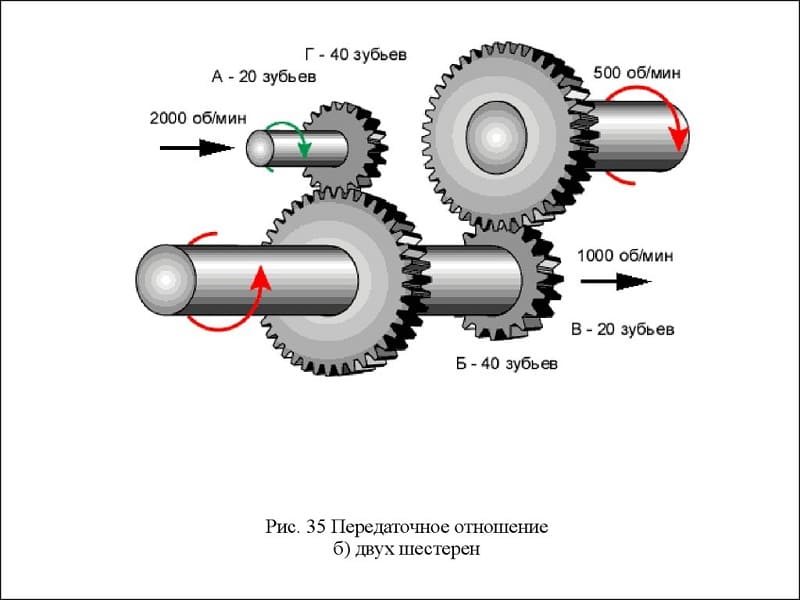
Итак, рассмотрим пример расчета с использованием двух шестерен.

Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.
В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.
Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.
Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.
Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.
Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.

Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.
В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.
Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.
Определим теперь частоту вращения.
Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.
Будем использовать формулу: S1 × T1 = S2 × T2,
S1 – частота вращения желтой (ведущей) шестерни,
Т1 – количество зубьев желтой (ведущей) шестерни;
S2- частота вращения красной шестерни,
Т2 – количество зубьев красной шестерни.
В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.
340 rpm × 7 = S2 × 40
Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.
Источник
Крутящий момент редуктора
Крутящий момент на выходном валу – вращающий момент на выходном валу. Учитывается номинальная мощность , коэффициент безопасности , расчетная продолжительность эксплуатации (10 тысяч часов), КПД редуктора.
Номинальный крутящий момент – максимальный крутящий момент, обеспечивающий безопасную передачу. Его значение рассчитывается с учетом коэффициента безопасности – 1 и продолжительность эксплуатации – 10 тысяч часов.
Максимальный вращающий момент – предельный крутящий момент, выдерживаемый редуктором при постоянной или изменяющейся нагрузках, эксплуатации с частыми пусками/остановками. Данное значение можно трактовать как моментальную пиковую нагрузку в режиме работы оборудования.
Необходимый крутящий момент – крутящий момент, удовлетворяющим критериям заказчика. Его значение меньшее или равное номинальному крутящему моменту.
Расчетный крутящий момент – значение, необходимое для выбора редуктора. Расчетное значение вычисляется по следующей формуле:
Mc2 = Mr2 x Sf ≤ Mn2
где Mr2 – необходимый крутящий момент; Sf – сервис-фактор (эксплуатационный коэффициент); Mn2 – номинальный крутящий момент.
Тип редуктора
Наличие кинематической схемы привода упростит выбор типа редуктора. Конструктивно редукторы подразделяются на следующие виды:
Червячный одноступенчатый со скрещенным расположением входного/выходного вала (угол 90 градусов).
Червячный двухступенчатый с перпендикулярным или параллельным расположением осей входного/выходного вала. Соответственно, оси могут располагаться в разных горизонтальных и вертикальных плоскостях.
Цилиндрический горизонтальный с параллельным расположением входного/выходного валов. Оси находятся в одной горизонтальной плоскости.
Цилиндрический соосный под любым углом. Оси валов располагаются в одной плоскости.
В коническо-цилиндрическом редукторе оси входного/выходного валов пересекаются под углом 90 градусов.
ВАЖНО! Расположение выходного вала в пространстве имеет определяющее значение для ряда промышленных применений
- Конструкция червячных редукторов позволяет использовать их при любом положении выходного вала.
- Применение цилиндрических и конических моделей чаще возможно в горизонтальной плоскости. При одинаковых с червячными редукторами массо-габаритных характеристиках эксплуатация цилиндрических агрегатов экономически целесообразней за счет увеличения передаваемой нагрузки в 1,5-2 раза и высокого КПД.
Таблица 1. Классификация редукторов по числу ступеней и типу передачи
| Тип редуктора | Число ступеней | Тип передачи | Расположение осей |
|---|---|---|---|
| Цилиндрический | 1 | Одна или несколько цилиндрических | Параллельное |
| 2 | Параллельное/соосное | ||
| 3 | |||
| 4 | Параллельное | ||
| Конический | 1 | Коническая | Пересекающееся |
| Коническо-цилиндрический | 2 | Коническая Цилиндрическая (одна или несколько) | Пересекающееся/скрещивающееся |
| 3 | |||
| 4 | |||
| Червячный | 1 | Червячная (одна или две) | Скрещивающееся |
| 1 | Параллельное | ||
| Цилиндрическо-червячный или червячно-цилиндрический | 2 | Цилиндрическая (одна или две) Червячная (одна) | Скрещивающееся |
| 3 | |||
| Планетарный | 1 | Два центральных зубчатых колеса и сателлиты (для каждой ступени) | Соосное |
| 2 | |||
| 3 | |||
| Цилиндрическо-планетарный | 2 | Цилиндрическая (одна или несколько) Планетарная (одна или несколько) | Параллельное/соосное |
| 3 | |||
| 4 | |||
| Коническо-планетарный | 2 | Коническая (одна) Планетарная (одна или несколько) | Пересекающееся |
| 3 | |||
| 4 | |||
| Червячно-планетарный | 2 | Червячная (одна) Планетарная (одна или несколько) | Скрещивающееся |
| 3 | |||
| 4 | |||
| Волновой | 1 | Волновая (одна) | Соосное |
Основные характеристики редуктора
Таковыми являются: тип передачи, тип зацепления, КПД, передаточное отношение, величина передачаемой мощности (номинальный крутящий момент на тихоходном валу и максимальные окружные скорости зубчатых колёс), число ступеней редукции.
Классификация редукторов по ГОСТу
Прежде всего редукторы классифицируются по типам механических передач: цилиндрические, конические, червячные, планетарные, волновые, спироидные и комбинированные.
Также редукторы можно классифицировать по типу корпусов, по способу охлаждения, по типам используемых подшипников, по скоростям вращения, передаточному числу; передаваемой мощности.
Корпуса редукторов
В серийном производстве широко распространены стандартизованные литые корпуса редукторов. Чаще всего в тяжёлой промышленности и машиностроении применяются корпуса из литейного чугуна, реже из литейных сталей. Когда требуется максимально облегчить конструкцию применяют легкосплавные корпуса. На корпусе редуктора чаще всего имеются места крепления — лапы и/или уши, за которые перемещают и/или крепят редукторы к основанию. На выходе валов располагают уплотнения для предотвращения вытекания масла. На корпусах редукторов зачастую располагают конструкционные элементы, предотвращающие увеличение давления внутри редуктора, возникающее от нагрева редуктора при его работе.
В штучном производстве широко используются сварные корпуса, позволяющие получать индивидуальные конструктивные решения.
Передаточное отношение
В дополнение к общему определению передаточного отношения, предполагающему отношение угловых скоростей ведущей и ведомого валов i=ω1ω2{\displaystyle i=\omega _{1}/\omega _{2}}, в любом механическом редукторе на зубчатых колёсах таковое может быть подсчитано без без замеров угловых скоростей по формулам, учитывающим число зубьев. Для определения передаточного отношения любого редуктора из двух взаимозацепленных зубчатых колёс, независимо от их формы и типа зацепления (цилиндрического, конического, гипоидного, червячного), верна формула вида z2z1{\displaystyle z_{2}/z_{1}} где z1{\displaystyle z_{1}} — число зубьев ведущего зубчатого колеса (число заходов червяка), а z2{\displaystyle z_{2}} — число зубьев ведомого зубчатого колеса. Передаточное отношение планетарного редуктора определить таким образом также возможно, хотя оно не имеет единой формулы подсчёта, и для его определения по числу зубьев всегда надо понимать, какое звено планетарного редуктора является ведущим/ведомым/опорным, а также учитывать тип и форму конкретного планетарного механизма.
Общее передаточное отношение всех редукторов, задействованных в конкретной кинематической цепи, равно произведению их передаточных отношений.
Редуктор со ступенчатым изменением передаточного отношения называется коробкой передач, с бесступенчатым — вариатор.
Звезды
Звезды бывают двух видов – передние (ведущие) и задние (ведомые). Передние звезды изготавливаются из стали или никель-хром-молибденового сплава. Они тоже бывают двух видов: стандарт и с канавками (с обеих сторон), по которым цепь выдавливает грязь.
Задние звезды отличаются по конструкции зуба и по материалу: сталь и алюминий. Стальные звезды более тяжелые, долговечные и дешевые, а алюминиевые легче и предпочтительнее из-за снижения неподрессоренных масс. Существуют также звезды с двумя контурами (комбинированные) и радиальные. Давайте подробней рассмотрим звезды на примерах нескольких мировых лидеров:
Тип редуктора
Наличие кинематической схемы привода упростит выбор типа редуктора. Конструктивно редукторы подразделяются на следующие виды:
Червячный одноступенчатый со скрещенным расположением входного/выходного вала (угол 90 градусов).
Червячный двухступенчатый с перпендикулярным или параллельным расположением осей входного/выходного вала. Соответственно, оси могут располагаться в разных горизонтальных и вертикальных плоскостях.
Цилиндрический горизонтальный с параллельным расположением входного/выходного валов. Оси находятся в одной горизонтальной плоскости.
Цилиндрический соосный под любым углом. Оси валов располагаются в одной плоскости.
В коническо-цилиндрическом редукторе оси входного/выходного валов пересекаются под углом 90 градусов.
ВАЖНО! Расположение выходного вала в пространстве имеет определяющее значение для ряда промышленных применений
- Конструкция червячных редукторов позволяет использовать их при любом положении выходного вала.
- Применение цилиндрических и конических моделей чаще возможно в горизонтальной плоскости. При одинаковых с червячными редукторами массо-габаритных характеристиках эксплуатация цилиндрических агрегатов экономически целесообразней за счет увеличения передаваемой нагрузки в 1,5-2 раза и высокого КПД.
Таблица 1. Классификация редукторов по числу ступеней и типу передачи
| Тип редуктора | Число ступеней | Тип передачи | Расположение осей |
| Цилиндрический | 1 | Одна или несколько цилиндрических | Параллельное |
| 2 | Параллельное/соосное | ||
| 3 | |||
| 4 | Параллельное | ||
| Конический | 1 | Коническая | Пересекающееся |
| Коническо-цилиндрический | 2 | Коническая Цилиндрическая (одна или несколько) | Пересекающееся/скрещивающееся |
| 3 | |||
| 4 | |||
| Червячный | 1 | Червячная (одна или две) | Скрещивающееся |
| 1 | Параллельное | ||
| Цилиндрическо-червячный или червячно-цилиндрический | 2 | Цилиндрическая (одна или две) Червячная (одна) | Скрещивающееся |
| 3 | |||
| Планетарный | 1 | Два центральных зубчатых колеса и сателлиты (для каждой ступени) | Соосное |
| 2 | |||
| 3 | |||
| Цилиндрическо-планетарный | 2 | Цилиндрическая (одна или несколько) Планетарная (одна или несколько) | Параллельное/соосное |
| 3 | |||
| 4 | |||
| Коническо-планетарный | 2 | Коническая (одна) Планетарная (одна или несколько) | Пересекающееся |
| 3 | |||
| 4 | |||
| Червячно-планетарный | 2 | Червячная (одна) Планетарная (одна или несколько) | Скрещивающееся |
| 3 | |||
| 4 | |||
| Волновой | 1 | Волновая (одна) | Соосное |
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
u12 = ± Z2/Z1 и u21 = ± Z1/Z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.
Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
u16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.
КПД зубчатой передачи
Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:
- трение соприкасаемых поверхностей;
- изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
- потери на шпонках и шлицах;
- трение в подшипниках.
Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.
При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.
muller1569 › Blog › Динамика разгона взависимости от размера и веса колеса.
Ежедневно мы уменьшаем-увеличиваем передаточное число, переключая КПП на передачу вверх-вниз.Помимо передаточного числа текущей передачи КПП, существует передаточное число главной пары — это постоянная величина, определяется соотношением зубьев шестерней передающих усилие от двигателя к КПП.Хотя гонщики меняют и эту характеристику для достижения, требуемого результата.
Поставив колесо меньшего диаметра R14, мы достигнем точно такого же результата, как если бы увеличили передаточное число главной пары. То есть за один оборот коленчатого вала машина пройдет меньшее расстояние. Увеличивая передаточное число мы заставляем автомобиль быстрее разгоняться по всему рабочему диапазону двигателя (1000 до 8000 об/мин) но теряем в максимальной скорости при максимальных оборотах.Поставив колесо меньшего диаметра R14, мы достигнем точно такого же результата, как если бы увеличили передаточное число главной пары. То есть за один оборот коленчатого вала машина пройдет меньшее расстояние. Увеличивая передаточное число мы заставляем автомобиль быстрее разгоняться по всему рабочему диапазону двигателя (1000 до 8000 об/мин) но теряем в максимальной скорости при максимальных оборотах.Например, если измерить разгон от 10 до 50 км/ч, то на первой передаче мы получим гораздо приятней результат, чем на второй. Если же будем стремиться к максимальной скорости, то тут вторая передача окажется фаворитом.Подобрав передаточное число главной пары (или поставив маленькое колесо) таким образом, чтобы на пятой передаче при максимальных оборотах скорость была 150км/ч мы получим существенно быстрый разгон до заданной скорости по сравнению со стоковым авто.Это я к тому что, вообще говоря, маленькие колеса динамику улучшают.
Есть такое понятие, как неподрессо́ренная ма́сса — применимо к наземным средствам передвижения, имеющим подвеску, которое обозначает массу, включающую массу колес и других деталей, крепящихся непосредственно к ним (дисков, шин, элементов тормозной системы, находящихся на колесе). Масса остальных элементов, удерживаемых над землей подвеской, называется подрессоренной массой.Есть такое понятие, как неподрессо́ренная ма́сса — применимо к наземным средствам передвижения, имеющим подвеску, которое обозначает массу, включающую массу колес и других деталей, крепящихся непосредственно к ним (дисков, шин, элементов тормозной системы, находящихся на колесе). Масса остальных элементов, удерживаемых над землей подвеской, называется подрессоренной массой.Соотношение подрессоренной и неподрессоренной массы имеет огромное значение, так как сила, с которой неподрессоренные компоненты воздействуют на автомобиль снизу вверх, должна компенсироваться весом подрессоренной массы. В противном случае автомобиль теряет сцепление с поверхностью дороги, что отрицательно сказывается на его управляемости. Для преодоления данной проблемы устанавливают облегченные диски и покрышки.
Кроме управляемости вес колес влияет и на динамику автомобиля. Так, чем тяжелее колеса, тем больше энергии и времени потребуется чтобы изменить скорость их вращения. То же относится и к процессу торможения. Однако, вклад энергии вращения колес в общую энергию движения автомобиля незначителен, и поэтому реально ощутить изменение в динамике разгона и торможения невозможно.
Соотношение неподрессоренных и подрессоренных масс в автомобиле составляет в среднем 1:15. Меняя это соотношение, можно добиться более высокой плавности хода автомобиля. Это соотношение можно изменить двумя способами: увеличив подрессоренную массу либо уменьшив неподрессоренную. Однако, если увеличивать подрессоренную массу, к примеру, загрузить по максимуму салон автомобиля, то разгонная динамика снизится. А вот уменьшив неподрессоренную массу, можно сохранить и даже улучшить динамику, добившись при этом высокой плавности хода. И добиться этого можно, только снизив вес колес. Снижение веса колёс на 1 килограмм с точки зрения динамики эквивалентно уменьшению массы в салоне автомобиля приблизительно на 1,5 кг. С точки зрения комфорта — на 10. Таким образом, если при замене дисков вы снижаете вес каждого всего на 2 килограмма (что в сумме дает 8 килограммов), то ваша машина будет ехать также плавно, как если бы в нее сел пассажир весом 80 кг., и так же быстро как будто из салона выкинули 15 кг а пассажир не садился вовсе.
Источник
Передаточное отношение зубчатой передачи
Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.
При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.
Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.
Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.
Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.
Передаточное отношение редуктора вычисляется по формуле:
где U12 – передаточное отношение шестерни относительно колеса;
ω1 и ω2 – угловые скорости ведущего и ведомого элемента соединения;
Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.